Computer Data Representation
We are always stunned by what computers do, which are seemingly miraculous things with all kinds of sounds, pictures, graphics, numbers, and text. It seems that we can build a replica of parts of our world inside the computer. You might think that this amazing machine is also amazingly complicated – it really is not. In fact, all of the wonderful multi-media that we see on modern computers is all constructed from simple ON/OFF switches – millions of them – but really nothing much more complicated than a switch. The trick is to take all of the real-world sound, picture, number etc data that we want in the computer and convert it into the kind of data that can be represented in switches, as shown in Figure 1.
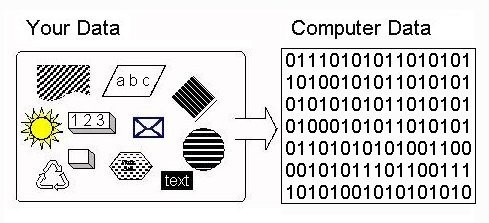
Figure 1: Representing Real-World Data In The Computer
Computers Are Electronic Machines. The computer uses electricity, not mechanical parts, for its data processing and storage. Electricity is plentiful, moves very fast through wires, and electrical parts fail much less frequently than mechanical parts. The computer does have some mechanical parts, like its disk drive (which are often the sources for computer failures), but the internal data processing and storage is electronic, which is fast and reliable (as long as the computer is plugged in).
Electricity can flow through switches: if the switch is closed, the electricity flows; if the switch is open, the electricity does not flow. To process real-world data in the computer, we need a way to represent the data in switches. Computers do this representation using a binary coding system.
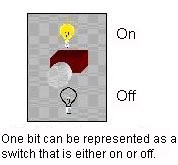
Binary and Switches. Binary is a mathematical number system: a way of counting. We have all learned to count using ten digits: 0-9. One probable reason is that we have ten fingers to represent numbers. The computer has switches to represent data and switches have only two states: ON and OFF. Binary has two digits to do the counting: 0 and 1 – a natural fit to the two states of a switch (0 = OFF, 1 = ON).
Bits and Bytes. One binary digit (0 or 1) is referred to as a bit, which is short for binary digit. Thus, one bit can be implemented by one switch, as shown in Figure 2. And in the table on the right, we see that bits can be grouped together into larger chunks to represent data:
| 0 | 1 bit |
| 1 | 1 bit |
| 0111 | 4 bits |
| 10110010 | 8 bits |
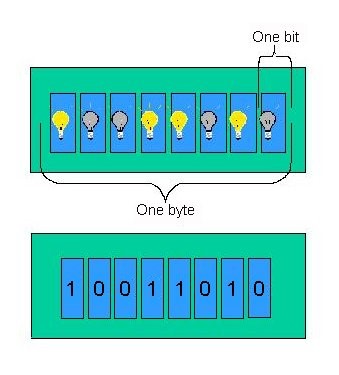
Figure 3: Byte implementation
Computer manufacturers express the capacity of memory and storage in terms of the number of bytes it can hold. The number of bytes can be expressed as kilobytes. Kilo represents 2 to the tenth power, or 1024. Kilobyte is abbreviated KB, or simply K. (K is used usually to mean 1000) A kilobyte is 1024 bytes. Thus, the memory of a 640K computer can store 640×1024, or 655,360 bytes. Memory capacity may also be expressed in terms of megabytes (1024×1024 bytes) or even gigabytes (1024x1024x1024 bytes). One megabyte, abbreviated MB, means roughly one million bytes. With storage devices, manufacturers sometimes express memory amounts in terms of gigabytes (abbreviated GB); a gigabyte is roughly a billion bytes. Computer memory, or RAM, in modern computers might hold 8GB (or even more), or roughly eight billion bytes. Modern computer hard disks hold several gigabytes (e.g. 750 GB) or even terabytes.
Representing Data in Bytes
Here is an important thing to keep in mind:
A single byte can represent many different kinds of data. What data it actually represents depends on how the computer uses the byte.
For instance, the byte: 01000011 can represent the integer 67, the character ‘C’, the 67th decibel level for a part of a sound, the 67th level of darkness for a dot in a picture, an instruction to the computer like “move to memory”, and other kinds of data too.
Integers. Integer numbers are represented by counting in binary.
Think for a minute how we count in decimal. We start with 0, and every new thing we count, we go to the next decimal digit. When we reach the end of the decimal digits (9), we use two digits to count by putting a digit in the “tens place” and then starting over again using our 10 digits. Thus, the decimal number 10 is a 1 in the “tens place” and a zero in the “ones place”. Eleven is a 1 in the “tens place” and a 1 in the “ones place”. And so on. If we need three digits, like 158, we use a third digit in the “hundred’s place”.
We do a similar thing to count in binary – except now we only have two digits: 0 and 1. So we start with 0, then 1, then we run out of digits, so we need to use two digits to keep counting. We do this by putting a 1 in the “two’s place” and then using our two digits. Thus two is 10 binary: a 1 in the “two’s place” and a 0 is the “one’s place”. Three is 11: a 1 in the “two’s place” and a 1 in the “one’s place”. We ran out of digits again! Thus, four is 100: a one in the “four’s place” a 0 in the “two’s place” a 0 in the “one’s place”.
What “places” we use depends on the counting system. In our decimal system, which we call Base 10, we use powers of 10. Ten to the zero power is 1, so the counting starts in the “one’s place”. Ten to the one power is 10, so the counting continues in the “ten’s place”. Ten to the second power (10 squared) is 100, so we continue in the “hundred’s place”. And so on. Binary is Base 2. Thus, the “places” are two to the zero power (“one’s place”), two to the one power (“two’s place”), two to the second power (“four’s place”), two to the third power (“eight’s place”), and so on.
When you look at a byte, the rightmost bit is the “one’s place”. The next bit is the “two’s place”, then the “four’s place”, then the “eight’s place”, and so on. So, when we said that the byte: 01000011 represents the decimal integer 67, we got that by adding up a 1 in the “ones place” and 1 in the “two’s place” and a 1 in the “64’s place” (two to the 6 power is 64). Add them up 1+2+64= 67.
The largest integer that can be represented in one byte is: 11111111 which is 128+64+32+16+8+4+2+1 = 255. Thus, the largest decimal integer you can store in one byte is 255. Computers use several bytes together to store larger integers.
The following table shows some binary counting and Decimal equivalents:
| Counting in Decimal-System | Counting in Binary |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
Characters. The computer also uses a single byte to represent a single character. But just what particular set of bits is equivalent to which character? In theory we could each make up our own definitions, declaring certain bit patterns to represent certain characters. Needless to say, this would be about as practical as each person speaking his or her own special language. Since we need to communicate with the computer and with each other, it is appropriate that we use a common scheme for data representation. That is, there must be agreement on which groups of bits represent which characters.
The code called ASCII (pronounced “AS-key”), which stands for American Standard Code for Information Interchange, uses 7 bits for each character. Since there are exactly 128 unique combinations of 7 bits, this 7-bit code can represent only characters. A more common version is ASCII-8, also called extended ASCII, which uses 8 bits per character and can represent 256 different characters. For example, the letter A is represented by 01000001. The ASCII representation has been adopted as a standard by the U.S. government and is found in a variety of computers, particularly minicomputers and microcomputers. The following table shows part of the ASCII-8 code.
Note that the byte: 01000011 does represent the character ‘C’.
| Character | Bit pattern | Byte
number |
Character | Bit pattern | Byte
number |
|
| A | 01000001 | 65 | ¼ | 10111100 | 188 | |
| B | 01000010 | 66 | . | 00101110 | 46 | |
| C | 01000011 | 67 | : | 00111010 | 58 | |
| a | 01100001 | 97 | $ | 00100100 | 36 | |
| b | 01100010 | 98 | \ | 01011100 | 92 | |
| o | 01101111 | 111 | ~ | 01111110 | 126 | |
| p | 01110000 | 112 | 1 | 00110001 | 49 | |
| q | 01110001 | 113 | 2 | 00110010 | 50 | |
| r | 01110010 | 114 | 9 | 00111001 | 57 | |
| x | 01111000 | 120 | © | 10101001 | 169 | |
| y | 01111001 | 121 | > | 00111110 | 62 | |
| z | 01111010 | 122 | ‰ | 10001001 | 137 |
Though not that important to know the ASCII representation of all characters, for reference purpose you can get the entire ASCII-8 table here
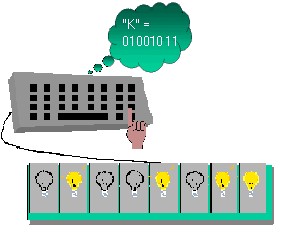
Figure 4: Character As a Byte
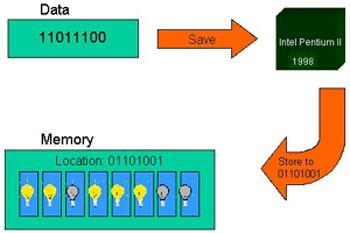
Figure 5: Character Byte Stored In Memory
If the person typed the word “CAT”, it would be represented by the following three bytes in the computer’s memory (think of it as three rows of eight switches in memory being ON or OFF):
| C | A | T |
| 01000011 | 01000001 | 01010100 |
